קיטוב הוא אחד המאפיינים הבסיסיים של אנטנות. ראשית עלינו להבין את הקיטוב של גלים מישוריים. לאחר מכן נוכל לדון בסוגים העיקריים של קיטוב אנטנה.
קיטוב ליניארי
נתחיל להבין את הקיטוב של גל אלקטרומגנטי מישורי.
לגל אלקטרומגנטי מישורי (EM) יש מספר מאפיינים. הראשון הוא שההספק נע בכיוון אחד (אין שינויים בשדה בשני כיוונים אורתוגונליים). שנית, השדה החשמלי והשדה המגנטי ניצבים זה לזה ואורטוגונליים זה לזה. שדות חשמליים ומגנטיים ניצבים לכיוון התפשטות הגל המישורי. כדוגמה, נבחן שדה חשמלי בתדר יחיד (שדה E) הניתן על ידי משוואה (1). השדה האלקטרומגנטי נע בכיוון +z. השדה החשמלי מכוון בכיוון +x. השדה המגנטי הוא בכיוון +y.
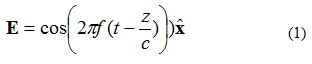
במשוואה (1), שימו לב לסימון: . זהו וקטור יחידה (וקטור בעל אורך), שאומר שנקודת השדה החשמלי נמצאת בכיוון x. הגל המישורי מודגם באיור 1.
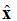
איור 1. ייצוג גרפי של השדה החשמלי הנע בכיוון +z.
קיטוב הוא צורת העקיבה וההתפשטות (קונטור) של שדה חשמלי. כדוגמה, נבחן את משוואת השדה החשמלי של גל מישורי (1). נבחן את המיקום שבו השדה החשמלי הוא (X,Y,Z) = (0,0,0) כפונקציה של הזמן. משרעת השדה מוצגת באיור 2, במספר מקרים בזמן. השדה מתנדנד בתדר "F".
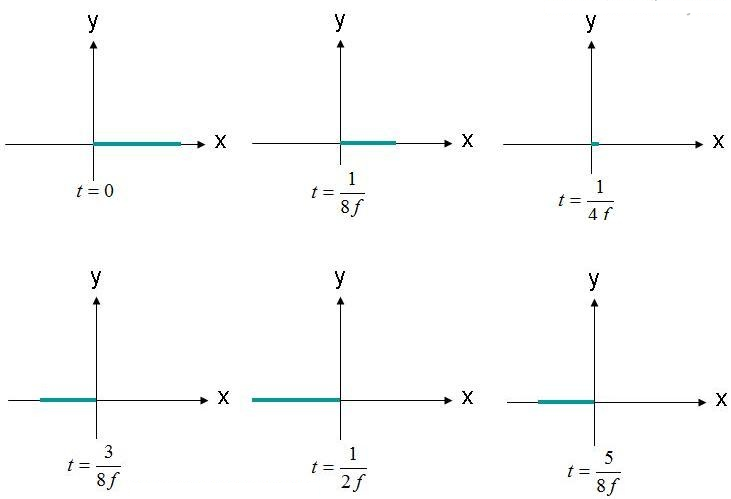
איור 2. התבונן בשדה החשמלי (X, Y, Z) = (0,0,0) בזמנים שונים.
השדה החשמלי נצפה במקור, כשהוא מתנדנד קדימה ואחורה במשרעת. השדה החשמלי נמצא תמיד לאורך ציר ה-x המצוין. מכיוון שהשדה החשמלי נשמר לאורך קו יחיד, ניתן לומר ששדה זה מקוטב באופן ליניארי. בנוסף, אם ציר ה-X מקביל לקרקע, שדה זה מתואר גם כמקטב אופקי. אם השדה מכוון לאורך ציר ה-Y, ניתן לומר שהגל מקוטב אנכית.
גלים מקוטבים ליניארית אינם צריכים להיות מכוונים לאורך ציר אופקי או אנכי. לדוגמה, גל שדה חשמלי עם אילוץ הנמצא לאורך קו כפי שמוצג באיור 3 יהיה גם מקוטב ליניארי.
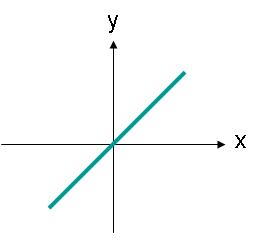
תמונה 3. משרעת השדה החשמלי של גל מקוטב ליניארית שמסלולו הוא זווית.
ניתן לתאר את השדה החשמלי באיור 3 באמצעות משוואה (2). כעת יש רכיב x ו-y של השדה החשמלי. שני הרכיבים שווים בגודלם.
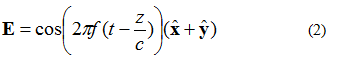
דבר אחד שיש לציין לגבי משוואה (2) הוא רכיב ה-xy והשדות האלקטרוניים בשלב השני. משמעות הדבר היא שלשני הרכיבים יש את אותה אמפליטודה בכל עת.
קיטוב מעגלי
כעת נניח שהשדה החשמלי של גל מישורי ניתן על ידי משוואה (3):
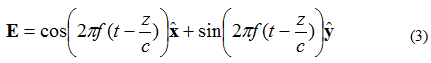
במקרה זה, אלמנטי ה-X וה-Y נמצאים ב-90 מעלות מחוץ לפאזה. אם השדה נצפה כ-(X, Y, Z) = (0,0,0) שוב כמו קודם, עקומת השדה החשמלי כנגד הזמן תופיע כפי שמוצג להלן באיור 4.
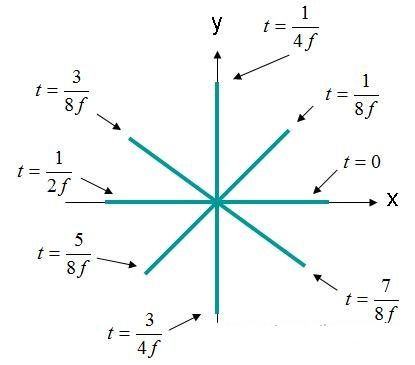
איור 4. עוצמת שדה חשמלי (X, Y, Z) = תחום EQ (0,0,0). (3).
השדה החשמלי באיור 4 מסתובב במעגל. סוג זה של שדה מתואר כגל מקוטב מעגלי. לקיטוב מעגלי, יש לעמוד בקריטריונים הבאים:
- תקן לקיטוב מעגלי
- לשדה החשמלי חייבים להיות שני רכיבים אורתוגונליים (אנכים).
- לרכיבים האורתוגונליים של השדה החשמלי חייבות להיות אמפליטודות שוות.
- רכיבי הריבוע חייבים להיות בזווית של 90 מעלות מחוץ לפאזה.
אם נעים על מסך גל איור 4, סיבוב השדה נחשב כנגד כיוון השעון ומקוטב מעגלי ימני (RHCP). אם השדה מסובב בכיוון השעון, השדה יהיה מקוטב מעגלי שמאלי (LHCP).
קיטוב אליפטי
אם לשדה החשמלי יש שני רכיבים ניצבים, בפער של 90 מעלות מהפאזה אך בעלי גודל שווה, השדה יהיה מקוטב בצורה אליפטית. בהתחשב בשדה החשמלי של גל מישורי הנע בכיוון +z, המתואר על ידי משוואה (4):
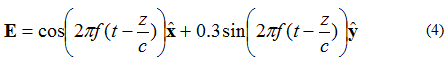
מוקד הנקודה שבה יגיע קצה וקטור השדה החשמלי ניתן באיור 5
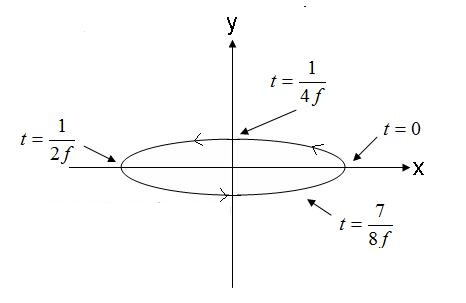
איור 5. שדה חשמלי של גל קיטוב אליפטי מהיר. (4).
השדה באיור 5, הנע נגד כיוון השעון, יהיה אליפטי ימני אם ינוע מחוץ למסך. אם וקטור השדה החשמלי מסתובב בכיוון ההפוך, השדה יהיה מקוטב אליפטי שמאלי.
יתר על כן, קיטוב אליפטי מתייחס לאקסצנטריות שלו. היחס בין האקסצנטריות למשרעת של הצירים הראשי והמשני. לדוגמה, האקסצנטריות של הגל ממשוואה (4) היא 1/0.3= 3.33. גלים מקוטבים אליפטית מתוארים עוד יותר על ידי כיוון הציר הראשי. למשוואת הגל (4) יש ציר המורכב בעיקר מציר x. שימו לב שהציר הראשי יכול להיות בכל זווית מישורית. הזווית אינה נדרשת להתאים לציר X, Y או Z. לבסוף, חשוב לציין שגם קיטוב מעגלי וגם קיטוב ליניארי הם מקרים מיוחדים של קיטוב אליפטי. גל מקוטב אליפטי אקסצנטרי 1.0 הוא גל מקוטב מעגלי. גלים מקוטבים אליפטית עם אקסצנטריות אינסופית. גלים מקוטבים ליניאריים.
קיטוב אנטנה
כעת, משאנו מודעים לשדות אלקטרומגנטיים של גלים מישוריים מקוטבים, הקיטוב של אנטנה מוגדר בפשטות.
קיטוב אנטנה - הערכה של שדה רחוק של אנטנה, הקיטוב של השדה המוקרן שנוצר. לכן, אנטנות רשומות לעתים קרובות כ"אנטנות מקוטבות ליניארית" או "אנטנות מקוטבות מעגליות ימניות".
מושג פשוט זה חשוב לתקשורת אנטנות. ראשית, אנטנה מקוטבת אופקית לא תתקשר עם אנטנה מקוטבת אנכית. עקב משפט ההדדיות, האנטנה משדרת ומקבלת בדיוק באותו אופן. לכן, אנטנות מקוטבות אנכית משדרות ומקבלות שדות מקוטבים אנכית. לכן, אם תנסו להעביר אנטנה מקוטבת אנכית ואופקית, לא תהיה קליטה.
במקרה הכללי, עבור שתי אנטנות מקוטבות ליניארית המסובבות זו ביחס לזו בזווית ( ), אובדן ההספק עקב אי-התאמה זו בקיטוב יתואר על ידי גורם אובדן הקיטוב (PLF):
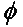
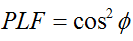
לכן, אם לשתי אנטנות יש קיטוב זהה, הזווית בין שדות האלקטרונים הקורנים שלהן היא אפס ואין אובדן הספק עקב אי התאמה בקיטוב. אם אנטנה אחת מקוטבת אנכית והשנייה מקוטבת אופקית, הזווית היא 90 מעלות, ולא יועבר הספק.
הערה: הזזת הטלפון מעל הראש לזוויות שונות מסבירה מדוע הקליטה לעיתים יכולה להשתפר. אנטנות טלפון סלולרי בדרך כלל מקוטבות באופן ליניארי, כך שסיבוב הטלפון יכול לעתים קרובות להתאים לקיטוב של הטלפון, ובכך לשפר את הקליטה.
קיטוב מעגלי הוא מאפיין רצוי של אנטנות רבות. שתיהן מקוטבות באופן מעגלי ואינן סובלות מאובדן אות עקב אי התאמה בקיטוב. אנטנות המשמשות במערכות GPS הן מקוטבות באופן מעגלי ימני.
כעת נניח שאנטנה מקוטבת ליניארית קולטת גלים מקוטבים מעגלית. באופן שווה, נניח שאנטנה מקוטבת מעגלית מנסה לקלוט גלים מקוטבים ליניארית. מהו גורם אובדן הקיטוב שנוצר?
נזכיר שקיטוב מעגלי הוא למעשה שני גלים אורתוגונליים מקוטבים ליניארית, ב-90 מעלות מחוץ לפאזה. לכן, אנטנה מקוטבת ליניארית (LP) תקבל רק את רכיב הפאזה של הגל המקוטב המעגלי (CP). לכן, לאנטנת LP יהיה אובדן אי-התאמה של קיטוב של 0.5 (-3dB). זה נכון ללא קשר לזווית שבה מסובבים את אנטנת ה-LP. לכן:
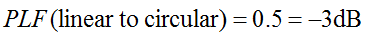
גורם אובדן הקיטוב מכונה לעיתים יעילות קיטוב, גורם אי-התאמה באנטנה או גורם קליטת אנטנה. כל השמות הללו מתייחסים לאותו מושג.
זמן פרסום: 22 בדצמבר 2023







