כשמדובר באנטנותהשאלה שמעניינת אנשים יותר מכל היא "כיצד באמת מושגת קרינה?" כיצד השדה האלקטרומגנטי שנוצר על ידי מקור האות מתפשט דרך קו ההולכה ובתוך האנטנה, ולבסוף "נפרד" מהאנטנה ויוצר גל חלל חופשי.
1. קרינה חד-תכליתית
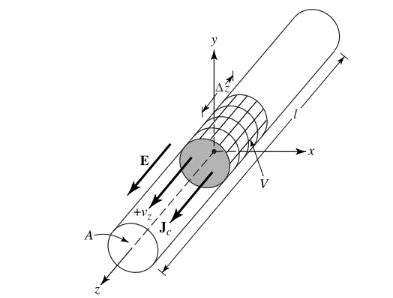
נניח שצפיפות המטען, המבוטאת כ-qv (קולומב/m3), מתפלגת באופן אחיד בחוט עגול בעל שטח חתך של a ונפח של V, כפי שמוצג באיור 1.
איור 1
המטען הכולל Q בנפח V נע בכיוון z במהירות אחידה Vz (מטר/שנייה). ניתן להוכיח שצפיפות הזרם Jz על חתך הרוחב של החוט היא:
Jz = qv vz (1)
אם החוט עשוי ממוליך אידיאלי, צפיפות הזרם Js על פני החוט היא:
Js = qs vz (2)
כאשר qs היא צפיפות המטען על פני השטח. אם החוט דק מאוד (באופן אידיאלי, הרדיוס הוא 0), ניתן לבטא את הזרם בחוט כך:
איז = ql vz (3)
כאשר ql (קולומב/מטר) הוא המטען ליחידת אורך.
אנו עוסקים בעיקר בחוטים דקים, והמסקנות חלות על שלושת המקרים הנ"ל. אם הזרם משתנה בזמן, הנגזרת של נוסחה (3) ביחס לזמן היא כדלקמן:
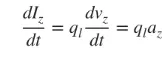
(4)
az היא תאוצת המטען. אם אורך החוט הוא l, ניתן לכתוב את (4) כך:
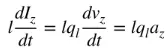
(5)
משוואה (5) היא הקשר הבסיסי בין זרם למטען, וגם הקשר הבסיסי של קרינה אלקטרומגנטית. במילים פשוטות, כדי לייצר קרינה, חייב להיות זרם או תאוצה (או האטה) של מטען המשתנה בזמן. בדרך כלל אנו מזכירים זרם ביישומים הרמוניים בזמן, ומטען מוזכר לרוב ביישומים חולפים. על מנת לייצר תאוצה (או האטה) של מטען, החוט חייב להיות כפוף, מקופל ולא רציף. כאשר המטען מתנדנד בתנועה הרמונית בזמן, הוא ייצר גם תאוצה (או האטה) של מטען מחזורי או זרם משתנה בזמן. לכן:
1) אם המטען לא זז, לא יהיה זרם ולא יהיה קרינה.
2) אם המטען נע במהירות קבועה:
א. אם החוט ישר ואורכו אינסופי, אין קרינה.
ב. אם החוט כפוף, מקופל או לא רציף, כפי שמוצג באיור 2, יש קרינה.
3) אם המטען מתנדנד לאורך זמן, המטען יקרין גם אם החוט ישר.
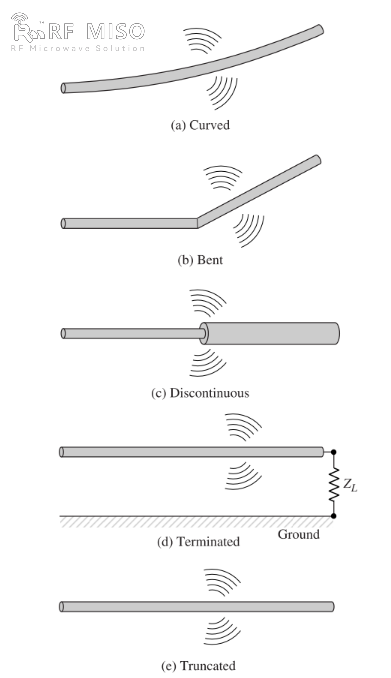
איור 2
הבנה איכותית של מנגנון הקרינה ניתנת להשגה על ידי התבוננות במקור פעימות המחובר לחוט פתוח שניתן להארקה באמצעות עומס בקצהו הפתוח, כפי שמוצג באיור 2(ד). כאשר החוט מופעל בתחילה, המטענים (אלקטרונים חופשיים) בחוט מופעלים על ידי קווי השדה החשמלי הנוצרים על ידי המקור. כאשר המטענים מואצים בקצה המקור של החוט ומאטים (תאוצה שלילית יחסית לתנועה המקורית) כאשר הם מוחזרים בקצהו, נוצר שדה קרינה בקצותיו ולאורך שאר החוט. האצת המטענים מושגת על ידי מקור כוח חיצוני שמניע את המטענים ומייצר את שדה הקרינה הנלווה. האטת המטענים בקצות החוט מושגת על ידי כוחות פנימיים הקשורים לשדה המושרה, הנגרמת על ידי הצטברות מטענים מרוכזים בקצות החוט. הכוחות הפנימיים צוברים אנרגיה מהצטברות המטען כאשר מהירותו יורדת לאפס בקצות החוט. לכן, האצת המטענים עקב עירור השדה החשמלי והאטת המטענים עקב אי-רציפות או עקומה חלקה של עכבת החוט הן המנגנונים ליצירת קרינה אלקטרומגנטית. למרות שגם צפיפות הזרם (Jc) וגם צפיפות המטען (qv) הן מונחי מקור במשוואות מקסוול, מטען נחשב לגודל בסיסי יותר, במיוחד עבור שדות חולפים. למרות שהסבר זה של קרינה משמש בעיקר עבור מצבים חולפים, ניתן להשתמש בו גם כדי להסביר קרינה במצב יציב.
ממליץ על כמה מצויניםמוצרי אנטנהמיוצר על ידיRFMISO:
2. קרינה דו-חוטית
חבר מקור מתח לקו תמסורת דו-מוליכי המחובר לאנטנה, כפי שמוצג באיור 3(א). הפעלת מתח על הקו הדו-מוליכי יוצרת שדה חשמלי בין המוליכים. קווי השדה החשמלי פועלים על האלקטרונים החופשיים (המופרדים בקלות מאטומים) המחוברים לכל מוליך ומאלצים אותם לנוע. תנועת המטענים מייצרת זרם, אשר בתורו מייצר שדה מגנטי.
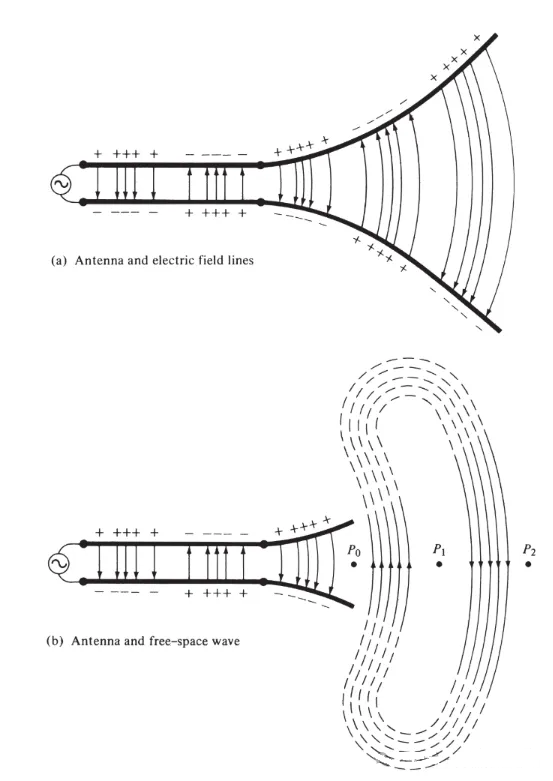
איור 3
קבלנו שקווי שדה חשמלי מתחילים במטענים חיוביים ומסתיימים במטענים שליליים. כמובן, הם יכולים גם להתחיל במטענים חיוביים ולהסתיים באינסוף; או להתחיל באינסוף ולהסתיים במטענים שליליים; או ליצור לולאות סגורות שאינן מתחילות ואינן מסתיימות במטענים כלשהם. קווי שדה מגנטי תמיד יוצרים לולאות סגורות סביב מוליכים נושאי זרם מכיוון שאין מטענים מגנטיים בפיזיקה. בנוסחאות מתמטיות מסוימות, מוצגים מטענים מגנטיים וזרמים מגנטיים שקולים כדי להראות את הדואליות בין פתרונות הכוללים מקורות חשמל ומגנטיים.
קווי השדה החשמלי המצוירים בין שני מוליכים עוזרים להראות את התפלגות המטען. אם נניח שמקור המתח הוא סינוסואידלי, אנו מצפים שהשדה החשמלי בין המוליכים יהיה גם הוא סינוסואידלי עם מחזור שווה לזה של המקור. הגודל היחסי של עוצמת השדה החשמלי מיוצג על ידי צפיפות קווי השדה החשמלי, והחצים מצביעים על הכיוון היחסי (חיובי או שלילי). יצירת שדות חשמליים ומגנטיים המשתנים בזמן בין המוליכים יוצרת גל אלקטרומגנטי המתפשט לאורך קו ההולכה, כפי שמוצג באיור 3(א). הגל האלקטרומגנטי נכנס לאנטנה עם המטען והזרם המתאים. אם נסיר חלק ממבנה האנטנה, כפי שמוצג באיור 3(ב), ניתן ליצור גל מרחב חופשי על ידי "חיבור" הקצוות הפתוחים של קווי השדה החשמלי (מוצגים בקווים המקווקווים). גל המרחב החופשי הוא גם מחזורי, אך נקודת הפאזה הקבועה P0 נעה החוצה במהירות האור ועוברת מרחק של λ/2 (ל-P1) בחצי מחזור זמן. ליד האנטנה, נקודת הפאזה הקבועה P0 נעה מהר יותר ממהירות האור ומתקרבת למהירות האור בנקודות רחוקות מהאנטנה. איור 4 מציג את התפלגות השדה החשמלי במרחב החופשי של אנטנת λ∕2 ב-t = 0, t/8, t/4 ו-3T/8.
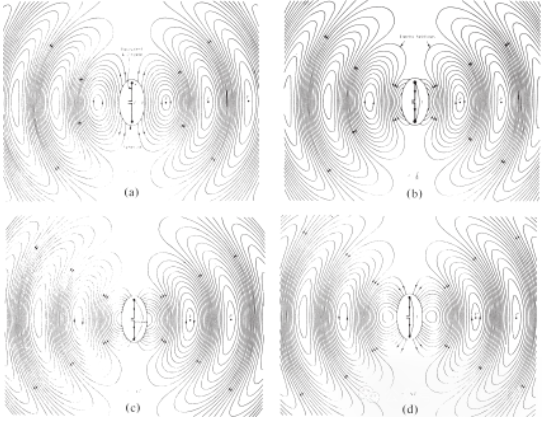
איור 4 התפלגות שדה חשמלי במרחב חופשי של אנטנת λ∕2 ב-t = 0, t/8, t/4 ו-3T/8
לא ידוע כיצד הגלים המודרכים מופרדים מהאנטנה ובסופו של דבר נוצרים כדי להתפשט במרחב החופשי. אנו יכולים להשוות גלי מודרכים וגלי מרחב חופשי לגלי מים, שיכולים להיגרם על ידי אבן שנפלה לגוף מים שקט או בדרכים אחרות. ברגע שההפרעה במים מתחילה, נוצרים גלי מים ומתחילים להתפשט החוצה. גם אם ההפרעה נפסקת, הגלים אינם נפסקים אלא ממשיכים להתפשט קדימה. אם ההפרעה נמשכת, נוצרים כל הזמן גלים חדשים, והתפשטותם של גלים אלה מפגרת אחרי הגלים האחרים.
אותו הדבר נכון לגבי גלים אלקטרומגנטיים הנוצרים מהפרעות חשמליות. אם ההפרעה החשמלית הראשונית מהמקור היא קצרת מועד, הגלים האלקטרומגנטיים הנוצרים מתפשטים בתוך קו ההולכה, לאחר מכן חודרים לאנטנה, ולבסוף מקרינים כגלי חלל חופשי, למרות שהעירור כבר אינו קיים (בדיוק כמו גלי המים וההפרעה שהם יצרו). אם ההפרעה החשמלית רציפה, הגלים האלקטרומגנטיים קיימים ברציפות ועוקבים אחריהם מקרוב במהלך ההתפשטות, כפי שמוצג באנטנה הדו-חרוטית המוצגת באיור 5. כאשר גלים אלקטרומגנטיים נמצאים בתוך קווי תמסורת ואנטנות, קיומם קשור לקיומו של מטען חשמלי בתוך המוליך. עם זאת, כאשר הגלים מוקרנים, הם יוצרים לולאה סגורה ואין מטען שישמור על קיומם. זה מוביל אותנו למסקנה ש:
עירור השדה דורש האצה והאטה של המטען, אך תחזוקת השדה אינה דורשת האצה והאטה של המטען.
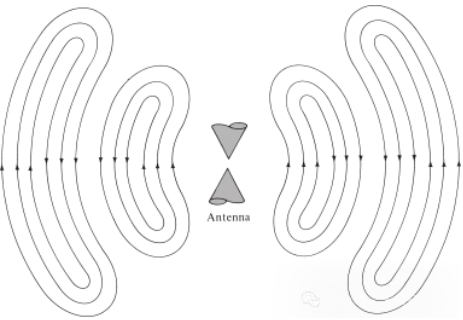
איור 5
3. קרינת דיפול
אנו מנסים להסביר את המנגנון שבאמצעותו קווי השדה החשמלי מתנתקים מהאנטנה ויוצרים גלי מרחב חופשי, ולקחת את האנטנה הדיפולרית כדוגמה. למרות שמדובר בהסבר פשוט, הוא גם מאפשר לאנשים לראות באופן אינטואיטיבי את יצירת גלי המרחב החופשי. איור 6(א) מציג את קווי השדה החשמלי הנוצרים בין שתי זרועות הדיפול כאשר קווי השדה החשמלי נעים החוצה ב-λ∕4 ברבע הראשון של המחזור. עבור דוגמה זו, נניח שמספר קווי השדה החשמלי שנוצרים הוא 3. ברבע הבא של המחזור, שלושת קווי השדה החשמלי המקוריים נעים ב-λ∕4 נוספים (סה"כ λ∕2 מנקודת ההתחלה), וצפיפות המטען על המוליך מתחילה לרדת. ניתן לראות אותה כנוצרת על ידי הכנסת מטענים מנוגדים, המבטלים את המטענים על המוליך בסוף המחצית הראשונה של המחזור. קווי השדה החשמלי הנוצרים על ידי המטענים המנוגדים הם 3 ונעים מרחק של λ∕4, המיוצג על ידי הקווים המקווקווים באיור 6(ב).
התוצאה הסופית היא שיש שלושה קווי שדה חשמלי כלפי מטה במרחק λ/4 הראשון ומספר זהה של קווי שדה חשמלי כלפי מעלה במרחק λ/4 השני. מכיוון שאין מטען נטו על האנטנה, קווי השדה החשמלי חייבים להיאלץ להיפרד מהמוליך ולהתאחד יחד ליצירת לולאה סגורה. זה מוצג באיור 6(c). במחצית השנייה, מתבצע אותו תהליך פיזיקלי, אך שימו לב שהכיוון הוא הפוך. לאחר מכן, התהליך חוזר על עצמו ונמשך ללא הגבלת זמן, ויוצר התפלגות שדה חשמלי בדומה לאיור 4.
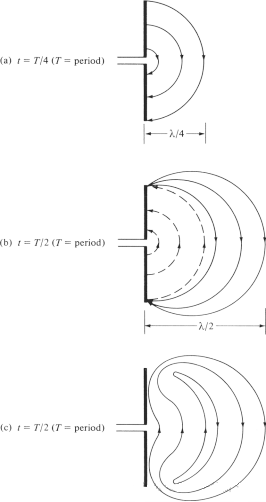
איור 6
למידע נוסף על אנטנות, אנא בקרו באתר:
זמן פרסום: 20 ביוני 2024










